![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)

a: Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên OBAC là tứ giác nội tiếp
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(4)
Từ (3),(4) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>BC\(\perp\)CD
mà OA\(\perp\)BC
nên OA//CD
c: Sửa đề: Đường thẳng qua O vuông góc với AD cắt BC tại E
Gọi H là giao điểm của BC và OA
Vì OA là đường trung trực của BC
nên OA\(\perp\)BC tại H và H là trung điểm của BC
Gọi I là giao điểm của OE và DA
Theo đề, ta có: OE\(\perp\)DA tại I
Xét ΔOIA vuông tại I và ΔOHE vuông tại H có
\(\widehat{IOA}\) chung
Do đó: ΔOIA~ΔOHE
=>\(\dfrac{OI}{OH}=\dfrac{OA}{OE}\)
=>\(OI\cdot OE=OH\cdot OA\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\left(2\right)\)
Từ (1),(2) suy ra \(OI\cdot OE=R^2=OD^2\)
=>\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)
Xét ΔOID và ΔODE có
\(\dfrac{OI}{OD}=\dfrac{OD}{OE}\)
\(\widehat{IOD}\) chung
Do đó: ΔOID~ΔODE
=>\(\widehat{OID}=\widehat{ODE}\)
=>\(\widehat{ODE}=90^0\)
=>DE là tiếp tuyến của (O)

Bài toán này là một bài toán năng suất điển hình, ta giải theo hướng truyền thống nhưng gãy gọn, dễ hiểu nha.
Gọi ẩn:
- Gọi số ngày An làm một mình để hoàn thành công việc là \(x\) (ngày).
⇒ Vậy số ngày Bình làm một mình sẽ là \(x + 9\) (vì Bình chậm hơn An 9 ngày).
Năng suất:
- Năng suất của An là \(\frac{1}{x}\) công việc/ngày.
- Năng suất của Bình là \(\frac{1}{x + 9}\) công việc/ngày.
Cả hai cùng làm thì xong sau 6 ngày:
⇒ Tổng năng suất:
\(\frac{1}{x} + \frac{1}{x + 9} = \frac{1}{6}\)Giải phương trình:
Nhân hai vế với \(6 x \left(\right. x + 9 \left.\right)\) để khử mẫu:
\(6 \left(\right. x + 9 \left.\right) + 6 x = x \left(\right. x + 9 \left.\right)\) \(6 x + 54 + 6 x = x^{2} + 9 x\) \(12 x + 54 = x^{2} + 9 x\) \(x^{2} - 3 x - 54 = 0\)Giải phương trình bậc hai:
\(x = \frac{3 \pm \sqrt{\left(\right. - 3 \left.\right)^{2} + 4 \cdot 54}}{2} = \frac{3 \pm \sqrt{9 + 216}}{2} = \frac{3 \pm \sqrt{225}}{2} = \frac{3 \pm 15}{2}\)→ \(x = 9\) (chọn nghiệm dương)
Vậy:
- An làm một mình hết 9 ngày.
- Bình làm một mình hết 18 ngày (vì chậm hơn 9 ngày).
Bây giờ:
An làm 3 ngày rồi nghỉ → An làm được:
\(\frac{3}{9} = \frac{1}{3} \&\text{nbsp};\text{c} \hat{\text{o}} \text{ng}\&\text{nbsp};\text{vi}ệ\text{c}\)⇒ Phần còn lại Bình làm:
\(1 - \frac{1}{3} = \frac{2}{3} \&\text{nbsp};\text{c} \hat{\text{o}} \text{ng}\&\text{nbsp};\text{vi}ệ\text{c}\)Bình làm 1 ngày được \(\frac{1}{18}\) công việc → thời gian để làm \(\frac{2}{3}\) công việc:
\(\frac{\frac{2}{3}}{\frac{1}{18}} = \frac{2}{3} \cdot 18 = 12 \&\text{nbsp};\text{ng} \overset{ˋ}{\text{a}} \text{y}\)✅ Đáp án: Bình cần 12 ngày để hoàn thành phần còn lại.
Nếu thích kiểu bài này thì mình có thể biến tấu thêm cho hợp vibe tranh truyện hay đố mẹo nha! 😎
Gọi thời gian An hoàn thành công việc khi làm một mình là x(ngày)
(Điều kiện: x>0)
Thời gian Bình cần để hoàn thành công việc khi làm một mình là: x+9(ngày)
Trong 1 ngày, An làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 ngày, Bình làm được: \(\dfrac{1}{x+9}\)(công việc)
Trong 1 ngày hai bạn làm được \(\dfrac{1}{6}\)(công việc)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{x+9}=\dfrac{1}{6}\)
=>\(\dfrac{x+9+x}{x\cdot\left(x+9\right)}=\dfrac{1}{6}\)
=>\(x\left(x+9\right)=6\left(2x+9\right)\)
=>\(x^2+9x-12x-54=0\)
=>\(x^2-3x-54=0\)
=>(x-9)(x+6)=0
=>\(\left[{}\begin{matrix}x-9=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\left(nhận\right)\\x=-6\left(loại\right)\end{matrix}\right.\)
Vậy: thời gian An hoàn thành công việc khi làm một mình là 9(ngày)
thời gian Bình hoàn thành công việc khi làm một mình là x+9=9+9=18(ngày)
Khi An làm một mình trong 3 ngày thì AN làm được: \(\dfrac{3}{x}=\dfrac{3}{9}=\dfrac{1}{3}\)(công việc)
=>Khối lượng công việc còn lại là \(1-\dfrac{1}{3}=\dfrac{2}{3}\)(công việc)
Thời gian Bình cần để hoàn thành phần còn lại là:
\(\dfrac{2}{3}:\dfrac{1}{18}=\dfrac{2}{3}\cdot18=\dfrac{36}{3}=12\left(ngày\right)\)

Đề lỗi rồi em, chỗ gọi I và M lần lượt là giao điểm của tia gì với (O) nhỉ?

a) Tính thể tích tối đa mà cốc có thể chứa:
Cốc nước có dạng hình trụ, vì vậy thể tích của cốc sẽ được tính bằng công thức thể tích của hình trụ:
\(V_{\text{c} \overset{ˊ}{\hat{\text{o}}} \text{c}} = \pi r^{2} h\)
Trong đó:
- \(r\) là bán kính đáy của cốc,
- \(h\) là chiều cao của cốc.
Cho trước:
- Bán kính đáy \(r = 2\) cm,
- Chiều cao \(h = 12\) cm.
Áp dụng công thức:
\(V_{\text{c} \overset{ˊ}{\hat{\text{o}}} \text{c}} = \pi \times 2^{2} \times 12 = \pi \times 4 \times 12 = 48 \pi \textrm{ } \text{cm}^{3}\)
Vậy thể tích tối đa mà cốc có thể chứa là:
\(V_{\text{c} \overset{ˊ}{\hat{\text{o}}} \text{c}} = 48 \pi \approx 150.8 \textrm{ } \text{cm}^{3}\)
b) Tính mực nước sau khi thả 6 viên bi vào cốc:
Bước 1: Tính thể tích của 6 viên bi:
Viên bi có dạng hình cầu, thể tích của một viên bi được tính theo công thức:
\(V_{\text{bi}} = \frac{4}{3} \pi r^{3}\)
Trong đó:
- \(r\) là bán kính của viên bi.
Cho trước bán kính viên bi là 1 cm, nên thể tích của một viên bi là:
\(V_{\text{bi}} = \frac{4}{3} \pi \times 1^{3} = \frac{4}{3} \pi \textrm{ } \text{cm}^{3}\)
Vậy thể tích của 6 viên bi là:
\(V_{\text{6}\&\text{nbsp};\text{bi}} = 6 \times \frac{4}{3} \pi = 8 \pi \textrm{ } \text{cm}^{3}\)
Bước 2: Tính mực nước dâng lên trong cốc:
Lượng nước trong cốc sẽ tăng lên do thể tích của các viên bi thả vào. Mỗi viên bi chiếm một thể tích của nước, nên mực nước trong cốc sẽ dâng lên một lượng nhất định.
Giả sử sau khi thả vào, mực nước dâng lên một khoảng \(h_{\text{d} \hat{\text{a}} \text{ng}}\). Mực nước này sẽ tạo thành một hình trụ có bán kính đáy là 2 cm và chiều cao là \(h_{\text{d} \hat{\text{a}} \text{ng}}\). Thể tích của phần nước dâng lên này chính là thể tích của 6 viên bi, tức là \(8 \pi \textrm{ } \text{cm}^{3}\).
Áp dụng công thức thể tích hình trụ để tính mực nước dâng lên:
\(V_{\text{d} \hat{\text{a}} \text{ng}} = \pi r^{2} h_{\text{d} \hat{\text{a}} \text{ng}}\)
Trong đó:
- \(r = 2\) cm (bán kính đáy của cốc),
- \(h_{\text{d} \hat{\text{a}} \text{ng}}\) là chiều cao mực nước dâng lên.
Thể tích nước dâng lên là \(8 \pi\), nên ta có:
\(8 \pi = \pi \times 2^{2} \times h_{\text{d} \hat{\text{a}} \text{ng}}\) \(8 \pi = 4 \pi \times h_{\text{d} \hat{\text{a}} \text{ng}}\)
Chia cả hai vế cho \(\pi\):
\(8 = 4 \times h_{\text{d} \hat{\text{a}} \text{ng}}\) \(h_{\text{d} \hat{\text{a}} \text{ng}} = 2 \textrm{ } \text{cm}\)
Kết quả:
Sau khi thả 6 viên bi vào cốc, mực nước trong cốc dâng lên 2 cm. Do đó, mực nước cách miệng cốc là:
\(12 - 8 - 2 = 2 \textrm{ } \text{cm}\)
Vậy mực nước cách miệng cốc 2 cm.

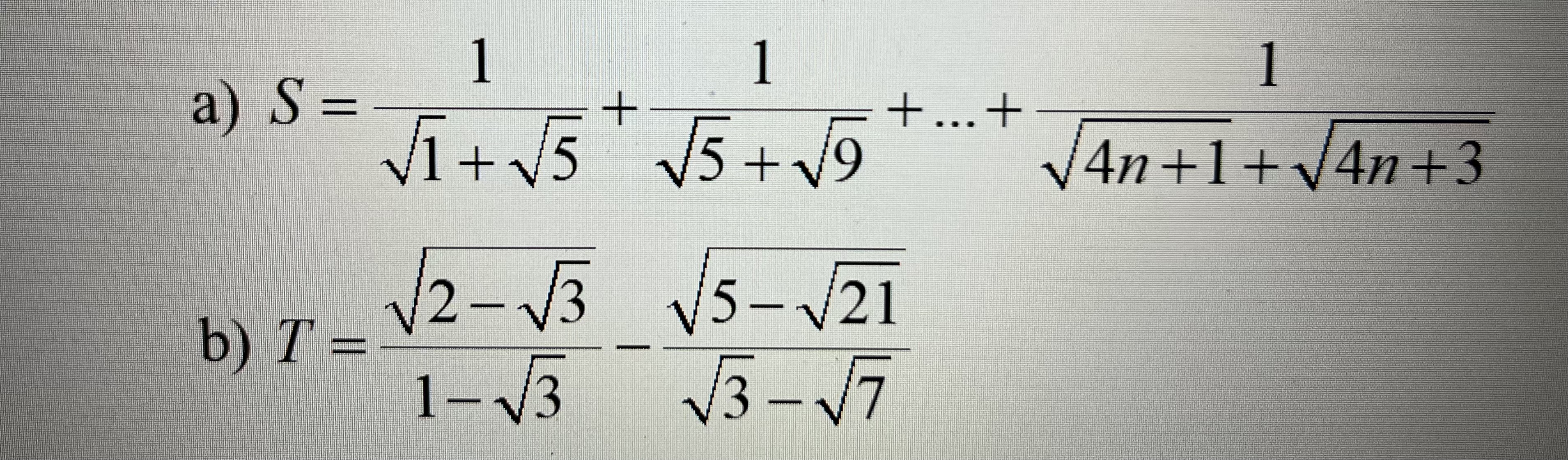
\(\text{Δ}=5^2-4\left(m-3\right)=25-4m+12=-4m+37\)
Để phương trình có hai nghiệm thì Δ>=0
=>-4m+37>=0
=>-4m>=-37
=>\(m< =\dfrac{37}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-5\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(2x_1x_2-\left(x_1+x_2\right)=2\)
=>\(2\left(m-3\right)-\left(-5\right)=2\)
=>2m-6+5=2
=>2m-1=2
=>2m=3
=>\(m=\dfrac{3}{2}\left(nhận\right)\)